conic

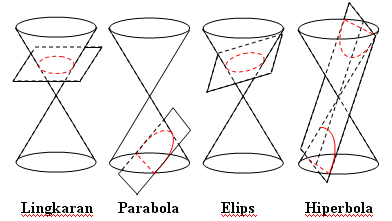
There are four kinds of conic sections: circle, parabola, ellipse, hyperbola

Definition
Circle
The circle is the locus of points equidistant to a certain point.
    * A certain point called the center of the circle
    * The same distance is called jari-jari/radius (r)

Area of ​​circle = π.r2 (r = radius)
Sample images:
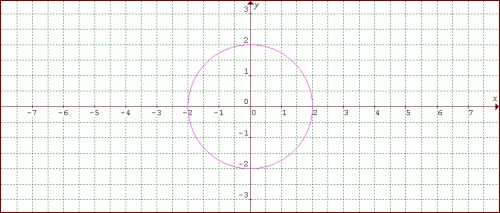
Circle with center (0, 0) and radius 2

Parabola
Parabola is the locus of points equidistant to a certain point and a line.

    * The point is called the focal point / station (F)
    * Particular line is called the line directress / line direction
    * The line through F and perpendicular to the direction of the line is called the axis of symmetry of the parabola
    * Point pieces parabola with axis of symmetry is called a parabolic peak
    * Shortest chord through Latus rectum → F is called perpendicular to the axis of symmetry

Sample images:
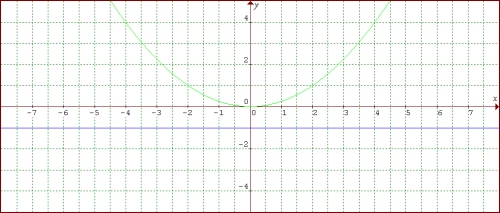
Horizontal parabola with a peak (0.0), focal (1, 0), and the direction of the line x = -1

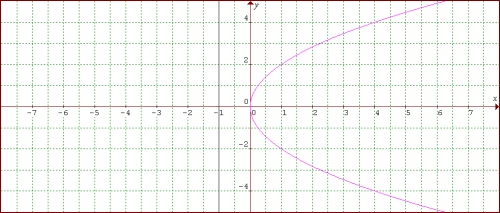
Vertical parabola with a peak (0.0), focus (0, 1), and the direction of the line y = -1

Ellipse
(1) ellipse is the locus of points whose distance to the number 2 point remains.

    * Total distance = 2a (for horizontal ellipses) or 2b (for vertical ellipse)
    * The two fixed points are called foci (F) → distance between F1 and F2 is 2c

(2) ellipse is the locus of all points whose distance ratio for a point and a fixed line = e (eksentrisitet), where 0 <e <1

    * It is the focal point (F), and the line is the line direction.
    * Line segment through both focus and cut the ellipse is called the major axis
    * Fitness elliptical is the midpoint of F1 and F2
    * Line segment through the center, perpendicular to the major axis and cut the ellipse is called the minor axis

Area of ​​ellipse = π.ab (horizontal length a = ½, b = ½ vertical length)
Sample images:
Horizontal ellipse with center (0, 0), the peak-peak (5, 0), (-5, 0), (0, 4), (0, -4), focus (3, 0), (-3, 0), and the line direction x = ± 25/3

Vertical ellipse with center (0, 0), the peak-peak (√ 2, 0), (- √ 2, 0), (0, 2), (0, -2), focus (0, √ 2), ( 0, - √ 2), and the direction of the line y = ± 2 √ 2/3

Hyperbola
(1) Hyperbole is the locus of points that the difference in distance to two fixed point

    * Difference distance = 2a (for horizontal ellipses) or 2b (for vertical ellipse)
    * The two fixed points are called foci (F) → distance between F1 and F2 is 2c

(2) Hyperbola is the locus of all points whose distance ratio for a point and a fixed line = e, where e> 1

    * Certain points are called foci (F1 and F2)
    * The line through the points F1 and F2 are called transverse axis (major axis) / real axis
    * Midpoint F1 and F2 are called hyperbolic center (P)
    * The line through P and perpendicular transverse axis is called the conjugate axis (axis adjacency) / imaginary axis
    * The points cut the hyperbole and called the transverse axis of the hyperbola apex
    * The line through the focus and perpendicular to the real axis and cut the hyperbole in the 2 point → line segment connecting the two points = Latus rectum

Sample images:
Horizontal hyperbola with center (0, 0), peak (2, 0), (-2, 0), focal (√ 6, 0), (- √ 6, 0) and asymptotes y = ± ½ √ 2 x

Vertical hyperbola with center (0, 0), peak (√ 2, 0), (- √ 2, 0), focus (0, √ 6), (0, - √ 6), and asymptotes y = ± ½ √ 2 x
x
Equation

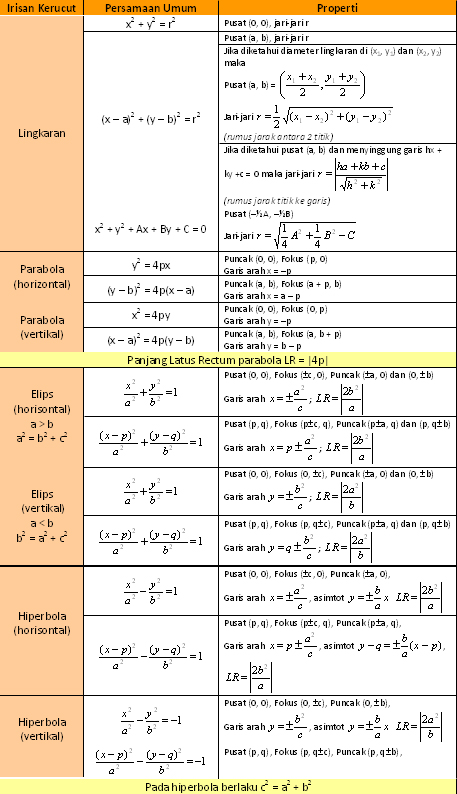
Tips!
How to distinguish the conic equations:

    * In the circle equation: x2 and y2 coefficients equal
    * In the parabolic equation: only one of the quadratic forms (only x2 or y2 only)
    * The ellipse equation: coefficient of x2 and y2 marked the same (both positive or both negative)
    * In Hyperbola equation: x2 and y2 coefficients of different signs (one positive, the other negative)

Example:

    * 3Y2 + 3x2 + 6x + y = 5 → Circle Equation
    * 3x2 + 6x + 3y = 5 → Parabola Equation
    * 3x2 + y2 + 6x + y = 5 → Ellipse Equation
    * 3x2 - 3Y2 + 6x + y = 5 → Hyperbola Equation


The point of the wedge notch Cones
How to find the position of a point on the cone:

   1. Make the right-hand side on the conic equation = 0
   2. Enter the coordinates of the point on the equation:

→ If the left-hand side <0 → point in the conic
→ If the left-hand side = 0 → point is right on the conic
→ If the right-hand side> 0 → beyond a point conic
Example:
Determine the position of the point (5, -1) of the ellipse with equation 3x2 + y2 + 6x + y = 5
How to:
3x2 + y2 + 6x + y - 5 = 0
The left: 3.52 + (-1) 2 + 6.5 + (-1) - 5 = 75 + 1 + 30 - 1 - 5 = 100
→ 100> 0, so the point (5, -1) is outside the ellipse

The status line of the wedge cone
How to find the position of the lines of the conic sections:

   1. The equation used line equation x = ... or y = ...
   2. Substituting equation of the line that the conic equation, resulting in a quadratic equation.
   3. Calculate the value of Discriminant (D) of the quadratic equation (remember! D = b2 - 4.ac)

→ If D <0 → line outside the conic
→ If D = 0 → offensive line conic in one point
→ If D> 0 → conic cut line at 2 points
Example:
Determine the position of the line x + 2y = 4 of the parabola with the equation 3x2 + 6x + 3y = 5
How to:
The line: x = 4 - 2y
3 (4 - 2y) 2 + 3y + 6 (4 - 2y) - 5 = 0
3 (16 - 16y + 4y2) + 3y + 24 - 12Y - 5 = 0
48 - 12y2 + 48y + 3y + 24 - 12Y - 5 = 0
12y2 - 57y + 67 = 0
D = b2 - 4.a.c = (-57) 2 - 04/12/67 = 33
Since D> 0, then the line x + 2y = 4 cut the parabola is

Tangent Equation
The equation of the tangent line with slope m

The equation of the tangent line at the point (x1, y1)
→ always use the system for justice:
(...) 2 into (...). (...)
(...) To ½ (...) + ½ (...)
On one of (...) will be the coordinates of a known point
→ enter into the equation results point to the fair

   1. If the point lies on the conic, will result in the equation of the tangent line
   2. If the point lies outside the conic sections, polar equation of the line will result in

Potongkan line with the polar conic sections to get a 2 point cut
Enter both point cut into the equation to get a fair result for two pieces of the equation of the tangent line

Example 1:
Determine the equation of the tangent to the circle x2 + y2 + 4x = 13 at the point (2, 1)
How to:
(2, 1) lies on the circle (22 + 12 + 4.2 = 13)
The equation for the fair:
x1.x y1.y + + + 2.x 2.x1 = 9
Enter the (2, 1) as x1 and y1:
1.y 2.x + + 2.2 + 2.x = 9
4x + y - 5 = 0 → equation of the tangent line

Example 2:
Determine the equation of the tangent to the circle x2 + y2 + 4x = 13 at the point (4, 1)
How to:
(4, 1) lie outside the circle (42 + 12 + 4.4 = 33> 16)
The equation for the fair:
x1.x y1.y + + + 2.x 2.x1 = 9
Enter the (4, 1) as x1 and y1:
1.y 4.x + + 4.2 + 2.x = 9
6x + y - 1 = 0 → polar equation of a line
y = 1 - 6x
Substituting into the equation of the line polar equation of a circle:
x2 + (1 - 6x) 2 + 4x - 13 = 0
x2 + 1 - 12x + 36x2 + 4x - 13 = 0
37x2 - 8x - 12 = 0
Use abc formula:

Enter the (x1, y1) and (x2, y2) into the equation for fair results